Mathematical / Theoretical Physics: Classical and Quantum Gravity, Quantum Information

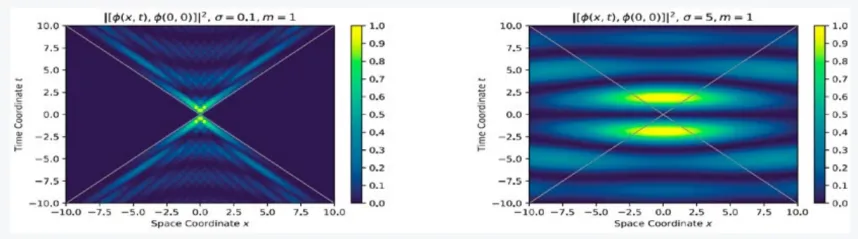
• Cosmology: We revisited the flatness and horizon problem of classical Friedmann-Lemaître cosmology (that are often used to support cosmological inflation) in the light of modern ideas on quantum geometry. Classical cosmology assumes the validity of General Relativity with its smooth Riemannian spacetime geometry at all scales — even below the Planck scale, where researchers expect quantum-gravitational effects to dominate. We have found that models that take quantum-gravitational effects and the resulting quantum geometry of spacetime below the Planck scale into account are quite generically not affected by the horizon problem of classical cosmology. A slight adjustment of the quantisation prescription of quantum field theory leads to models with the required symmetries and expected effects of quantum geometry including fuzzy light cones and non-locality. Preliminary computations show that in these models not only the horizon problem but also the flatness problem may be resolved.
• Generalized geometry: Generalized geometry provides a powerful mathematical setting for the formulation of gravity theories. Since it naturally incorporates stringy symmetries, it is useful in deriving the low-energy effective gravity actions of string theory, where it allows us to bypass complicated computations in a target space approach. We have contributed to the development of differential geometric methods in this field and have computed effective actions in general backgrounds. In this effort, we have pioneered an approach based on graded super geometry, out of which the objects and relations of generalized geometry arise as derived structures.
• Particle physics and gravity: In related work, we have found a systematic way to formulate actions for bosonic (tensor) particles in a unified fashion. This includes the wellknown Lovelock and Horndeski classifications of gravity theories. As an application, we have investigated the gravitational analog of axion electrodynamics with a parity-violating gravitoelectromagnetic theta term. We have shown that this term leads to potentially observable effects, namely corrections to the Lense-Thirring effect and to the propagation of gravitational waves that are more than 80 orders of magnitude stronger than that of the much more familiar gravitational Chern-Simons term quadratic in curvature.

• We constructed a non-local quantum field theory toy model that can describe important aspects of quantum geometry in the context of cosmology.
• We discovered a unified description of bosonic field theories including gravity in the framework of graded super geometry.
• We predicted a new strong topological gravitational effect with potential for astrophysical observation.
• We developed new coherent state entropy-based methods to analyze the cosmic microwave background (CMB) that are particularly sensitive to non-Gaussianities in the data, are very efficient in computing resources, and have their origin in our research on quantum information theory.

DFGResearch Training Group “Models of Gravity”, with PhD students, BSc students, visitors.

• A. Chatzistavrakidis, G. Karagiannis, G. Manolakos, P. Schupp. Axion gravitodynamics, Lense-Thirring effect, and gravitational waves. Physical Review D. 2022. 
• P. Schupp. Wehrl entropy, coherent states and quantum channels. The Physics and Mathematics of Elliott Lieb, Vol. II, EMS Press, Berlin. 2022. 
• A. Chatzistavrakidis, G. Karagiannis, P. Schupp. Torsion-induced gravitational theta-term and gravitoelectromagnetism. The European Physical Journal C. 2020. 
• A. Chatzistavrakidis, G. Karagiannis, P. Schupp. A unified approach to standard and exotic dualizations through graded geometry. Communications in Mathematical Physics. 2020. 
• M. Minkov, M. Pinkwart, P. Schupp. Entropy methods for CMB analysis of anisotropy and non-Gaussianity. Physical Review D. 2019.